
Equitability measures
SIMPSON"S INDEX
Assume we have a collection of N individuals w/ s spp. and Ni
individuals in the ith species
Select 2 individuals at random: if Prob [indivs. are of same sp.] is
high, then community is not diverse
| e.g.,: | Community
I has 5 species w/ 10 individuals each |
| | Community
II has 1 species w/ 42 indivs, 4 species w/ 2 indivs each
- cI =
- cII =
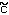 I = I =
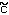 II
= II
=
|
- c = Prob[2 randomly-selected individuals are of the same
species]
- probability loses interpretability w/ non-count data
(e.g., basal cover) unless they are converted to
relative abundance values (i.e., pi)
- Note that increased diversity --> decreased Prob[2 indivs. being
of same spp.]
- therefore, 1-c is sometimes used to express diversity
- Also, 1/
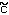 = no. of
equally abundant spp. necessary to produce same diversity as that
observed in the sample
= no. of
equally abundant spp. necessary to produce same diversity as that
observed in the sample
- e.g., 1/
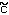 I =
1/0.2 = 5.0 species
I =
1/0.2 = 5.0 species1/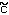 II
= 1/0.712 = 1.4 species
II
= 1/0.712 = 1.4 species
- c is most affected by the importance values of the first few
dominant spp.
- e.g., 0.92 = 0.81 (common
sp.)
0.12 = 0.01 (rare sp.)
- the latter sp. contributes little to the sum
- thus, Simpson's has been called a dominance index
(affected primarily by few dominant spp.)
- c is relatively insensitive to sampling variability if sample is
adequate to represent dominant spp.
Assumptions of Simpson's index:
- all spp. in pop'n are represented in sample
- there is a pop'n of size N from which we can draw an
infinite number of samples w/o replacement (i.e., pop'n
is infinitely large)
- these samples represent random samples of the pop'n
SHANNON'S INDEX (syn. Shannon-Weaver, Shannon-Wiener index)
- Assumptions identical to Simpson's index
- Prob[selecting an indiv. of ith sp.] = Ni/N
- Prob[selecting 2 indivs. of ith sp.] =
(Ni/N)2
- Prob[selecting all Ni indivs. of ith sp.] =
(Ni/N)Ni
- Prob[selecting all Ni indivs. of all s spp.]
= p =
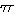 (Ni/N)Ni
(Ni/N)Ni
= (N1/N)N ×
(N2/N)N × ... ×
(Ns/N)N
- H' = -ln p = N(lnN) -
 [Ni(lnNi)]
[Ni(lnNi)]
- H' is Shannon's index
| e.g., | Species | Collection I | Collection II |
| | 1 | 6 | 12 |
| | 2 | 3 | 6 |
| | 3 | 1 | 2 |
| | Total | 10 | 20 |
- note that richness and proportions are identical in the
two collections
- HI' = 10ln10 - (6ln6 + 3ln3 + 1ln1) = 8.979
- HII' = 20ln20 - (12ln12 + 6ln6 + 2ln2) =
17.958
- therefore H' = f(n), an undesirable
characteristic
- use proportions of spp.:
- HI' = HII' = 1ln1 - (.6ln.6
+ .3ln.3 + .1ln.1) = 0.8979
- but ln1 = 0, so H' simplifies to H' = -
 pilnpi,
where pi = Ni/N
pilnpi,
where pi = Ni/N
- eH' is interpreted as the number of equally
abundant spp. necessary to produce the same diversity (H') as
observed in sample
- e.g., from previously examples
- Community I has s = 5,
N1=N2=N3=N4=N5=10
- Community II has s = 5, w/ Ni = 42 and
N2=N3=N4=N5=2
- HI' = -(10/50)ln(10/50) × 5 = 1.6094
- HII' = -{(42/50)ln(42/50) + [(2/50)ln(2/50) × 4]} =
0.66147
- eH' = e1.6094 = 5
- eH' = e0.66147 = 1.937
- Behavior of H'
- H' is sensitive to changes in rare spp.
- H' is logarithmically related to s
- Whittaker preferred H' for ease of calculation and
interpretation, esp. compared to indices developed later
- Both Simpson's index and Shannon's index are widely use to
describe communities
- Pielou (mathematical ecologist) does not believe that Shannon's
index has any theoretical basis, because plants are not
distributed randomly. H' (like c) assumes:
- well-defined "parent" pop'n that can be sampled at
random
- all spp. in pop'n are represented in sample
- Pielou: perhaps the sample (i.e., quadrat) is not a sample
of "something bigger" (e.g., pop'n), but rather a
measurement of something that exists on a local
scale
Pielou pointed out that Simpson's index and Shannon's index are
not appropriate measures of equitability if the sample (i.e.,
quadrat) is not a sample of "something bigger" (e.g., pop'n), but
rather a measurement of something that exists on a local scale.
So she suggested Brillouin's index (H) for calculating
equitability on a local scale
- This measure is to be interpreted on the basis of pop'n, where
sample = pop'n
- There is no way to normalize H
| e.g., | Abundance of | Community
A | Community B |
| | Species
1 | 3 | 6 |
| | Species
2 | 4 | 8 |
| | Species
3 | 3 | 6 |
| | | s=3, N=10 | s=3,
N=20 |
- same proportions in each collection
(i.e., same richness-abundance
relations)
- HA =
- HB =
- Thus, H is dependent on N
- "Normalized" HA' = HB' =
- A further disadvantage of H is that it can "behave"
strangely
| e.g., | | Community A: | s=10,
N=50; N1=N2=...=N10=5 |
| | | Community B: | s=9,
N=1000; N1=N2=...=N8=110,
N9=120 |
| | | HA = | |
| | | H'A = - pilnpi
= pilnpi
= | |
| | | HB = | |
| | | H'B = - pilnpi pilnpi | |
- Thus, the collection w/ more spp. and greater evenness
is A, as reflected by H' but not by H
- H is rarely used (despite the mathematical advantages),
because:
- it depends on N
- it behaves strangely, sometimes
- it is difficult to employ
- The rarity w/ which H is used reflects the idea that the decision
of which index to use must be based on more than theoretical
grounds--ease and interpretability of application are important
- McIntosh's Index is based on a geometric model:
- u =
 (
( Ni2)
Ni2)
- e.g., N=7; N1=3,
N2=4
- u =
 (
( Ni2)
=
Ni2)
=  (32
+ 42) = 5 = length of vector from
origin
(32
+ 42) = 5 = length of vector from
origin
- e.g., N=10; N1=2, N2=3,
N3=5
- u =
 (
( Ni2)
=
Ni2)
=  (22
+ 32 + 52) = 6.1644
(22
+ 32 + 52) = 6.1644
| Interpretation: | For a given N, u will be maximum when all
individuals belong to one species (in this
case, u = N); i.e., monoculture, w/ minimum
diversity, has maximum u |
| | For
a given N, u will be minimum when each
individual belongs to a different species (in
this case, u =  N); i.e.,
maximum diversity has minimum u N); i.e.,
maximum diversity has minimum u |
- From this, McIntosh defined an equitability index:
- M = N - u
- An obvious disadvantage is that M = f(N); however, M can be
normalized (Peet 1974):
- M' = M/Mmax = (N-u)/(N-
 N)
N)
- But M' behaves strangely:
- e.g., Collection A: s=3, N=10, N1=2,
N2=3, N3=5
- Collection B: s=3, N=20, N1=4, N2=6,
N3=10
- These collections have identical richness and
diversity relations, but have different
M':
- M'A =
- M'B =
- A transformation can be applied to correct this problem
(Pielou):
- M'' = M/[N-(N/
 s)]
s)]
- For our example, Ma =
- Mb =
- Note M'' = f(evenness) only; richness (s) does not affect
M''
- 0
 M''
M''  1
1
- Other equitability measures proposed by Pielou and commonly used
in the early 1970's (but not much now):
- J' = H'/H'max, where
- H' = Shannon's index and
- H'max = ln(s) (i.e., J' = observed diversity/max.
diversity for that no. of spp.)
- J = H/Hmax, where
- H = Brilloun's index and
- Hmax =
- Disadvantages:
- Dependent on sample area or number of species (and
number of species must be known)
- Division by H'max or Hmax,
which was intended to "adjust" for richness, does not:
- Alatalo (1981, Oikos 37:199-204) showed that
J'
and J increase for purely mathematical
reasons w/
increasing richness
- given s species, w/ half equally abundant and
the other half "indefinitely rare"
(Alatalo
doesn't define this):
| | s | 2 | 4 | 50 | 100 | 1000 |
| | J | 0 | .5 | .7 | .82 | .90 |
- Thus, although dominance-diversity relations
are constant, J ranges from 0 to 1 depending
on richness of sample
- Alatalo proposed an equitability index, E
- E =
- E does not require an estimate of richness
Dominance/diversity models
Graphics
The number of species in a community and the relative abundance
of each species are integral and intrinsic properties of
communities. These properties lead to theories about aspects of
community organization.
Now, the question that emerges is: where do these diversity
relationships come from?
Niche pre-emption model
Suppose the percent of total available resources used by a
species is determined by the species' success in pre-empting for
its own use some portion of available resources
Less successful spp. utilize resources that are left. And so on,
for all spp.
Graphically, w/ k=0.5:
| In model: let | I1 = importance value of most successful
sp., |
| |
I2 = I.V. of 2nd-most important sp., and so on ... |
| | Is = I.V. of least successful sp. |
| |  Ii =
N Ii =
N |
e.g., given k = 0.4:
| Sp. i | Resources available | Resources
pre-empted by sp. i | Ii/Ii-1
= c | k = 1-c = Ii/res.
avail. |
| 1 | 100 | 40 | -- | -- |
| 2 | 60 | 24 | 24/40 = 0.6 | 24/60 =
0.4 |
| 3 | 36 | 14.4 | 14.4/24 = 0.6 | 14.4/36 =
0.4 |
| 4 | 21.6 | 8.64 | 8.64/14.4 =
0.6 | 8.64/21.6 = 0.4 |
| 5 | 12.96 | 5.184 | 0.6 | 0.4 |
| . | | | | |
| . | | | | |
| . | | | | |
| s | | | | |
 =
100
=
100
| Ii =
Nk(1-k)i-1; e.g., | I1 =
100(.4)(1-.4)1-1 = 40 |
| | I2 = 100(.4)(1-.4)2-1 = 24 |
| Note Ii =
Nk(1-k)i-1 = I1ci-1; e.g., | I1 = 40(.6)1-1 = 40 |
| | I2 = 40(.6)2-1 = 24 |
This model predicts that spp. importance values look like
this:
Question: do they really?
- Conclusion: this model appears to represent reality in:
- coniferous spp. of low species richness; e.g.,:
- Frasier fir forest (GSMNP)
- pine-heath forest
- pygmy conifer-oak scrub type (AZ)
- early-successional stages of old-field succession
- may be appropriate for some strata not very rich in
spp. even though community as a whole is not geometric
(i.e., strata w/in a community)
- in "severe" environments
- In these situations, dominance tends to be strongly
developed, and spp. may be related in resource use thru
strong competitive interactions
More
graphics
If the relative abundances of spp. are governed by relatively
independent factors, then we might expect the relative
importances of spp. to be approx. normally-distributed
- Note that old-field succession tends to: [Whittaker 1972,
Taxon 21:213-251]
- geometric -------> log-normal -------> increased dominance by
- trees -------> steepening of log-normal distribution
- According to May (1975 in Cody and Diamond, eds., Ecology and
Evolution of Communities):
- ... the lognormal distribution is associated with [results]
of random variables, and factors that influence large and
heterogeneous assemblies of species indeed tend to do so in
this fashion.
- ... if the environment is randomly fluctuating, or
alternatively as soon as several factors become significant
..., we expect the statistical Law of Large Numbers to take
over and produce the ubiquitous lognormal distribution.
- Colinvaux (1986 Ecology text, p. 676):
- Log-normal populations result when the abundance of each
species pop'n is determined at random relatively
independently of other species populations. The prevalence
of log-normal distributions shows that the relative
distributions of animals and plants very often is determined
by random processes.
- Thus, interactions appears to be less important in the lognormal
model than in the niche pre-emption (geometric series) model
- The log-normal model may be expected in relatively spp.-rich
communities where many factors (which are largely
independent) influence spp. performance
- Broken-stick model
- Pr = (N/s)
 [1/(s-i+1)],
where
[1/(s-i+1)],
where
- s = no. spp.,
- N = no. individuals,
- i = spp. sequence from least to most important, and
- Pr = I.V. of sp. n in sequence from least important
(i=1) thru sp. in question
- e.g., given N=100 individuals of s=3 spp.,
| Spp. | Pr |
| 1 | (100/3)[1/(3-1+1)] = 11.1 |
| 2 | (100/3)[1/(3-1+1) + 1/(3-2+1) = 27.8 |
| 3 | (100/3)[1/(3-1+1) + 1/(3-2+1) + 1/(3-3+1)] = 61.1 |
Note  Pr = Pr =
| 100 |
- Acc. to May (1975), this model is applicable to communities
comprising a limited number of taxonomically similar spp. ...
(Colinvaux 1986 refers to spp. of a guild)
- ... in competitive contact w/ each other in a relatively
homogeneous habitat; in this situation, a more structured pattern
of relative abundances of spp. (other than that resulting from
conditions associated w/ log-normal distribution) may be
expected. The basic picture is one of intrinsically even
resource division of some major environmental resource. In this
model, species are limited by competition at randomly located
boundaries.
Previous
lectureNext
lecture
 Ni(Ni-1)]/[N(N-1)],
where N = total pop'n size and Ni = indivs in ith
species
Ni(Ni-1)]/[N(N-1)],
where N = total pop'n size and Ni = indivs in ith
species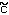 =
=  (Ni/N)2
(Ni/N)2
 Ni(Ni-1)]/[N(N-1)],
where N = total pop'n size and Ni = indivs in ith
species
Ni(Ni-1)]/[N(N-1)],
where N = total pop'n size and Ni = indivs in ith
species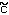 =
=  (Ni/N)2
(Ni/N)2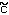 = no. of
equally abundant spp. necessary to produce same diversity as that
observed in the sample
= no. of
equally abundant spp. necessary to produce same diversity as that
observed in the sample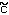 I =
1/0.2 = 5.0 species
I =
1/0.2 = 5.0 species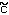 II
= 1/0.712 = 1.4 species
II
= 1/0.712 = 1.4 species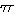 (Ni/N)Ni
(Ni/N)Ni [Ni(lnNi)]
[Ni(lnNi)] pilnpi,
where pi = Ni/N
pilnpi,
where pi = Ni/N pilnpi
=
pilnpi
= pilnpi
pilnpi (
( Ni2)
Ni2) (
( Ni2)
=
Ni2)
=  (32
+ 42) = 5 = length of vector from
origin
(32
+ 42) = 5 = length of vector from
origin (
( Ni2)
=
Ni2)
=  (22
+ 32 + 52) = 6.1644
(22
+ 32 + 52) = 6.1644 N); i.e.,
maximum diversity has minimum u
N); i.e.,
maximum diversity has minimum u N)
N) s)]
s)] M''
M''  1
1 Ii =
N
Ii =
N =
100
=
100 [1/(s-i+1)],
where
[1/(s-i+1)],
where Pr =
Pr =